Las 10 paradojas matemáticas y físicas más famosas

Si algo destaca la inteligencia humana es por la necesidad de llegar a conclusiones lógicas a partir de razonamientos que sabemos que son válidos. Nos sentimos a gusto cuando, por ejemplo, sabiendo que las personas que viven en Francia son franceses y que, si París es una ciudad en Francia, las personas que viven en París son francesas.

Y así con miles y millones de razonamientos, pues hemos creado un sistema que nos permite vivir tranquilos sabiendo que si utilizamos las normas lógicas, llegaremos a soluciones perfectamente válidas e incuestionables.

Ahora bien, hay veces en las que, ya sea de forma real o más habitualmente de forma hipotética, la lógica no funciona y entramos de lleno en la formulación de una paradoja, que es una situación en la que, pese a usar los razonamientos lógicos de siempre, llegamos a una conclusión sin sentido o que rompe con lo que consideremos válido.

Una paradoja es aquello que sucede cuando nuestra mente no es capaz de encontrar la lógica a una conclusión, incluso sabiendo que hemos realizado razonamientos correctos. En el artículo de hoy, pues, prepárate para poner tu cerebro a prueba con algunas de las paradojas más famosas y que seguro que te hacen estallar la mente.

• Te recomendamos leer: “Los 21 tipos de lógica (y sus características)”

¿Cuáles son las paradojas más célebres de las Matemáticas y la Física?

Las paradojas pueden desarrollarse en cualquier forma de conocimiento, pero las más asombrosas e impactantes son, sin duda, las matemáticas y las físicas. Hay veces que los razonamientos matemáticos, pese a ser perfectamente lógicos, nos hacen llegar a conclusiones que, incluso viendo que hemos seguido las normas, se escapan totalmente de lo que nosotros consideramos verídico o, valga la redundancia, lógico.

Desde los tiempos de la Antigua Grecia con los filósofos más importantes hasta las investigaciones actuales sobre mecánica cuántica, la historia de la ciencia está llena de paradojas que o bien no tienen solución posible (ni tendrán) o esta escapa totalmente de lo que dicta nuestra lógica. Empecemos.

1. Paradoja de los gemelos

Propuesta por Albert Einstein para explicar las implicaciones de la Relatividad General, esta es una de las paradojas físicas más famosas. Su teoría, entre otras muchas cosas, afirmaba que el tiempo era algo relativo que depende del estado de movimiento de dos observadores.

En otras palabras, en función de la velocidad a la que te muevas, el tiempo, respecto a otro observador, pasará más deprisa o más lento. Y cuanto más deprisa te muevas, más lento pasará el tiempo; respecto a un observador que no llega a estas velocidades, claro.

Por ello, esta paradoja dice que si cogemos a dos gemelos y a uno de ellos lo montamos en una nave espacial que alcanza velocidades cercanas a la velocidad de la luz y otro lo dejamos en la Tierra, cuando el viajero estelar regresara, vería que es más joven que el que se ha quedado en la Tierra.

2. Paradoja del abuelo

La paradoja del abuelo también es una de las más famosas, pues no tiene solución. Si construyéramos una máquina del tiempo, viajáramos al pasado y matáramos a nuestro abuelo, nuestro padre no habría nacido nunca y, por lo tanto, nosotros tampoco. Pero, entonces, ¿cómo habríamos viajado al pasado? No tiene solución porque, básicamente, los viajes al pasado son imposibles por las leyes de la física, así que este quebradero de cabeza se queda en algo hipotético.

• Te recomendamos leer: “Ciencia y cine: ¿hay ciencia real en las películas?”

3. Paradoja del gato de Schrödinger

La paradoja del gato de Schrödinger es una de las más célebres en el mundo de la Física. Formulada en 1935 por el físico austríaco Erwin Schrödinger, esta paradoja intenta explicar lo complejo del mundo cuántico en lo que a naturaleza de partículas subatómicas se refiere.

La paradoja propone una situación hipotética en la que ponemos a un gato en una caja, dentro de la cual hay un mecanismo conectado a un martillo con un 50% de probabilidades de romper un frasco de veneno que mataría al gato.

En este contexto, de acuerdo a las leyes de la mecánica cuántica, hasta que no abramos la caja, el gato estará vivo y muerto a la vez. Solo cuando la abramos observaremos uno de los dos estados. Pero hasta que no se haga, ahí dentro, según la cuántica, el gato está tanto vivo como muerto.

• Para saber más: “El gato de Schrödinger: ¿qué nos dice esta paradoja?”

4. Paradoja de Möbius

La paradoja de Möbius es una de carácter visual. Diseñada en 1858, se trata de una figura matemática imposible desde nuestra perspectiva tridimensional. Consiste en una banda plegada pero que tiene una superficie de una sola cara y un solo borde, por lo que no cuadra con nuestra distribución mental de los elementos.

5. Paradoja del cumpleaños

La paradoja del cumpleaños nos dice que, si en una habitación hay 23 personas, hay una probabilidad del 50,7% de que como mínimo dos de ellas cumplan años el mismo día. Y con 57, la probabilidad es del 99,7%. Se trata de algo contraintuitivo, pues seguramente pensamos que hacen falta muchas más personas (cercanas a 365) para que esto suceda, pero las matemáticas no engañan.

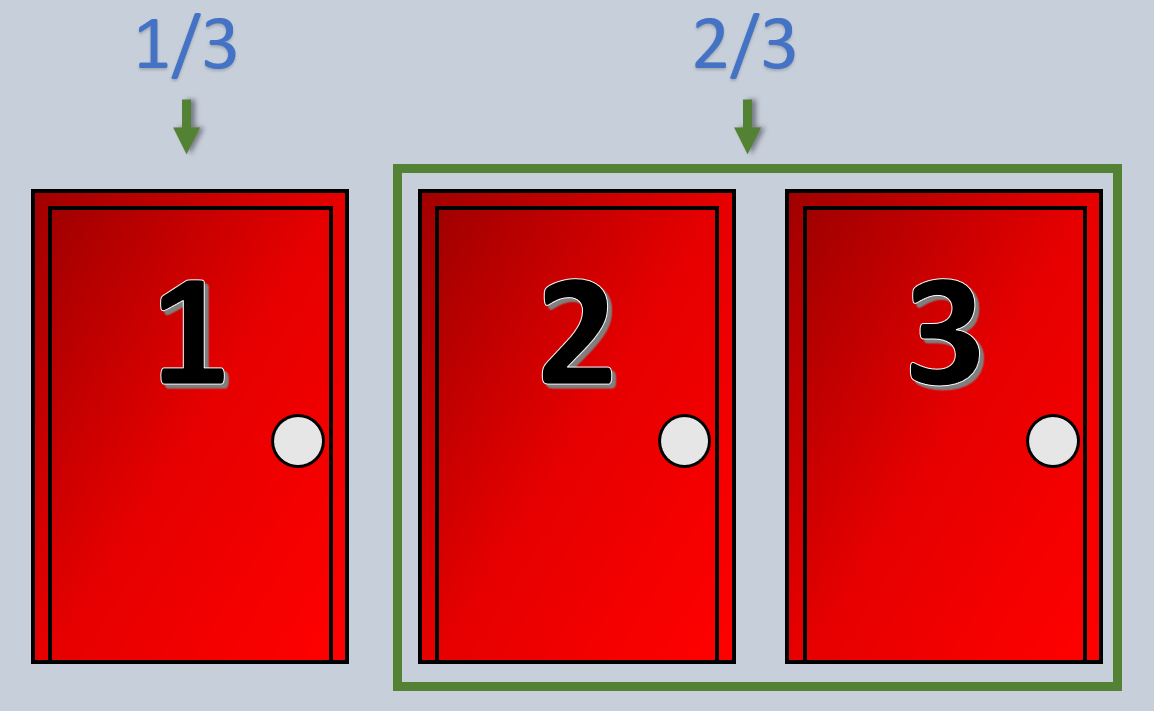
6. Paradoja de Monty Hall

Nos ponen tres puertas cerradas delante, sin saber qué hay detrás de ellas. Detrás de una de ellas, hay un coche. Si abres esa puerta correcta, te lo llevas. Pero detrás de las otras dos, te espera una cabra. Solo hay una puerta con el premio y no hay ninguna pista.

Entonces, elegimos una al azar. Al hacerlo, la persona que sabe qué hay detrás, abre una de las puertas que no has elegido y vemos que hay una cabra. En ese momento, esa persona nos pregunta si queremos cambiar de elección o si nos mantenemos con la misma puerta.

¿Cuál es la decisión más correcta? ¿Cambiar de puerta o mantenernos con la misma elección? La paradoja de Monty Hall nos dice que, aunque pueda parecer que las probabilidades de ganar no deberían cambiar, sí lo hacen.

De hecho, la paradoja nos enseña que lo más inteligente es cambiar de puerta porque al principio, tenemos ⅓ de probabilidades de acertar. Pero cuando la persona abre una de las puertas, altera las probabilidades, se actualizan. En este sentido, las probabilidades de que la puerta inicial sea la correcta siguen siendo de ⅓, mientras que la otra puerta restante tiene una probabilidad de ½ de ser la elegida.

Cambiando, pasas de tener una probabilidad de acertar del 33% a tener una del 50%. Aunque parezca imposible que cambien las probabilidades después de que nos hagan elegir de nuevo, las matemáticas, de nuevo, no engañan.

7. Paradoja del hotel infinito

Imaginemos que somos el dueño de un hotel y queremos construir el más grande del mundo. Al principio, pensamos en hacer uno de 1.000 habitaciones, pero es posible que alguien lo supere. Lo mismo pasa con 20.000, 500.000, 1.000.000…

Por ello, llegamos a la conclusión de que lo mejor (todo a nivel hipotético, claro) es construir uno con habitaciones infinitas. El problema es que en un hotel infinito que se llena de infinitos huéspedes, las matemáticas nos dicen que quedaría abarrotado.

Esta paradoja nos dice que para solucionar este problema, cada vez que entrara un nuevo huésped, los que ya había antes se tenían que desplazar a la siguiente habitación, es decir, sumando 1 a su número actual. De este modo, se resuelve el problema y cada nuevo huésped se hospeda en la primera habitación del hotel.

En otras palabras, la paradoja nos dice que, en un hotel con infinitas habitaciones, solo puedes hospedar a infinitos huéspedes si estos entran en la habitación número 1, pero no en la número infinito.

8. Paradoja de Teseo

La paradoja de Teseo nos hace cuestionarnos si, tras reemplazar todas y cada una de las partes de un objeto, este sigue siendo el mismo. Esta paradoja, de imposible solución, nos hace preguntarnos acerca de nuestra identidad humana, pues todas nuestras células se regeneran y son sustituidas por nuevas, por lo tanto, ¿seguimos siendo la misma persona desde que nacemos hasta que morimos? ¿Qué es lo que nos da identidad? Sin duda, una paradoja sobre la que reflexionar.

• Quizás te interese: “¿Cómo se regeneran las células humanas?”

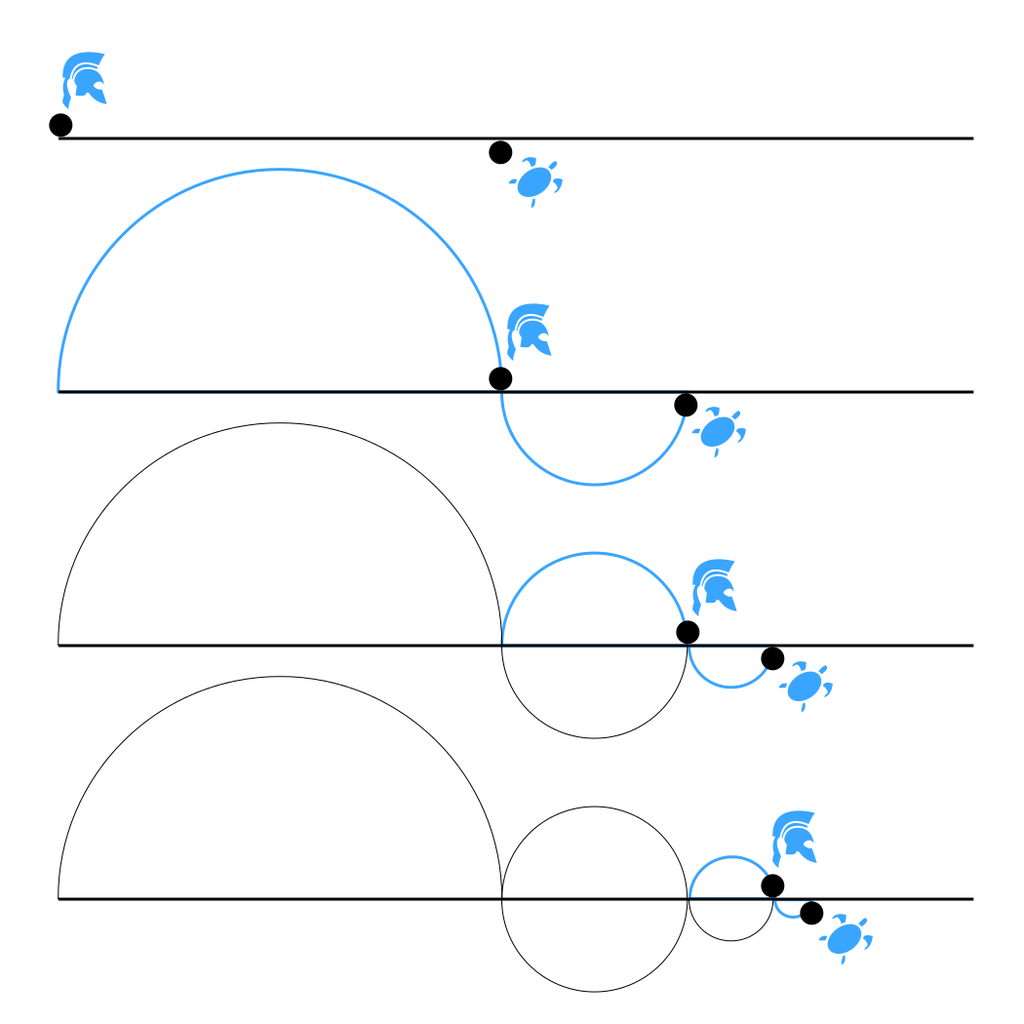
9. Paradoja de Zenón

La paradoja de Zenón, también conocida como paradoja del movimiento, es una de las más célebres del mundo de la Física. Tiene bastantes formas distintas, pero una de las más famosas es la de Aquiles y la tortuga.

Imaginemos que Aquiles reta a una tortuga a una carrera de 100 metros (menudo espíritu competitivo), pero decide darle una ventaja. Tras darle este margen, Aquiles sale corriendo. En muy poco tiempo, llega donde estaba la tortuga. Pero cuando llega, la tortuga ya habrá llegado a un punto B. Y cuando Aquiles llegue a B, la tortuga llegará al punto C. Y así hasta el infinito, pero sin nunca alcanzarla. Cada vez habrá menos distancia que les separe, pero jamás la atrapará.

Evidentemente, esta paradoja solo sirve para plantear cómo tienen lugar las series infinitas de números, pero en la realidad, está claro que Aquiles hubiera superado sin problemas a la tortuga. Por eso es una paradoja.

10. Paradoja de Russell

Imaginemos un pueblo en el que hay la norma de que todo el mundo tiene que ir afeitado, solo hay un barbero, por lo que van bastante cortos de este servicio. Por ello, y con el fin de no saturarlo y de que todo el mundo pueda ir afeitado, se pone la norma de que el barbero solo puede afeitar a aquellas personas que no puedan afeitarse por sí solas.

Entonces, el barbero se encuentra con un problema. Y es que si se afeita, estará demostrando que puede afeitarse por sí solo, pero entonces estará rompiendo con la norma. Pero si no se afeita, romperá también con la norma de ir afeitado. ¿Qué tiene que hacer el barbero? Exacto, estamos ante una paradoja.